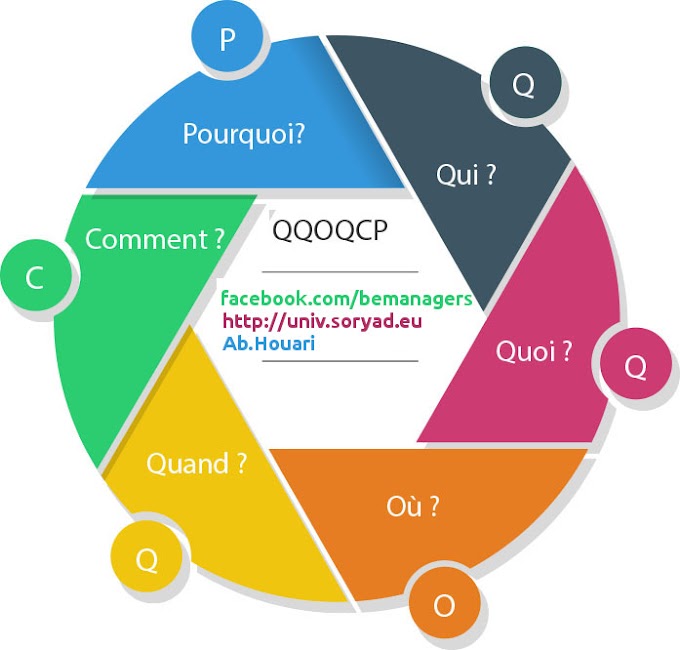
1- C'est quoi une Carte de Contrôle?
2- Comment Construire une Carte de contrôle ?
3- Les cartes de contrôle sous Excel
- 4- Les Cartes de contrôle sous Minitab :
5- Les différentes cartes de contrôle :
Les enjeux du contrôle
Au-delà du prix de vente, la satisfaction du client passe de manière incontournable par la qualité du produit. Pour assurer la qualité spécifiée, il est nécessaire de contrôler le produit fabriqué
Les méthodes
Il existe 2 grandes méthodes de contrôle :
♦ Le contrôle à 100% : chaque produit est contrôlé individuellement de façon manuelle ou automatisée, ce qui permet une identification de toutes les non conformités et l’éjection de chaque produit mauvais
♦ Le contrôle statistique par MSP (Maîtrise Statistique des Procédés) qui est basé sur l’échantillonnage : les décisions (acceptation, refus) sont prises sur la base de l’analyse d’une petite partie de la production : l’échantillon.
La carte de contrôle est un outil parmi d’autres au service de la MSP.
Les différentes cartes de contrôle
Les cartes de contrôle se présentent sous différentes formes :
Cartes aux valeurs (les échantillons comportent des mesures numériques)
♦ Carte en X et R : on étudie la moyenne et l’étendue
♦ Carte en X et S : on étudie la moyenne et l’écart type
♦ Carte à la moyenne mobile (pour des échantillons de taille 1)
Cartes aux attributs (les jugements se limitent à Bon/Mauvais par des contrôles souvent visuels)
♦ Carte des proportions de non conformes (carte nP)
♦ Carte des nombres de non conformes (carte C)
♦ Carte des nombres de défauts
Le principe
La carte montre le graphique des valeurs au fil du temps (échantillon par échantillon)
Pour chaque carte, on calcule des limites supérieures et inférieures (à l’intérieur des tolérances)
On analyse le comportement des valeurs (la manière dont elles évoluent)
On en tire des conclusions sur l’efficacité de la production.
Au-delà du prix de vente, la satisfaction du client passe de manière incontournable par la qualité du produit. Pour assurer la qualité spécifiée, il est nécessaire de contrôler le produit fabriqué
Les méthodes
Il existe 2 grandes méthodes de contrôle :
♦ Le contrôle à 100% : chaque produit est contrôlé individuellement de façon manuelle ou automatisée, ce qui permet une identification de toutes les non conformités et l’éjection de chaque produit mauvais
♦ Le contrôle statistique par MSP (Maîtrise Statistique des Procédés) qui est basé sur l’échantillonnage : les décisions (acceptation, refus) sont prises sur la base de l’analyse d’une petite partie de la production : l’échantillon.
La carte de contrôle est un outil parmi d’autres au service de la MSP.
Les différentes cartes de contrôle
Les cartes de contrôle se présentent sous différentes formes :
Cartes aux valeurs (les échantillons comportent des mesures numériques)
♦ Carte en X et R : on étudie la moyenne et l’étendue
♦ Carte en X et S : on étudie la moyenne et l’écart type
♦ Carte à la moyenne mobile (pour des échantillons de taille 1)
Cartes aux attributs (les jugements se limitent à Bon/Mauvais par des contrôles souvent visuels)
♦ Carte des proportions de non conformes (carte nP)
♦ Carte des nombres de non conformes (carte C)
♦ Carte des nombres de défauts
Le principe
La carte montre le graphique des valeurs au fil du temps (échantillon par échantillon)
Pour chaque carte, on calcule des limites supérieures et inférieures (à l’intérieur des tolérances)
On analyse le comportement des valeurs (la manière dont elles évoluent)
On en tire des conclusions sur l’efficacité de la production.
Exemple de carte X-R (Moyenne - Étendue)
On prélève 11 échantillons (au rythme de 1 échantillon toutes les 2 heures). Chaque
échantillon (prélèvement) contient 4 produits (Taille de l'échantillon n= 4 éléments).
les poids mesurés des produits de chaque échantillon sont présentés dans le tableau suivant :
Etape 1: Pour chaque échantillon on calcule sa valeur moyenne et son étendue (rappel : l’étendue est la différence entre la plus grande et la plus petite des valeurs)
Etape 2 : Calculer la moyenne des moyennes et des étendues
échantillon (prélèvement) contient 4 produits (Taille de l'échantillon n= 4 éléments).
les poids mesurés des produits de chaque échantillon sont présentés dans le tableau suivant :
| Échantillons | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Élément 1 | 64 | 62 | 64 | 64 | 67 | 67 | 62 | 62 | 65 | 69 | 64 |
| Élément 2 | 65 | 63 | 64 | 65 | 63 | 70 | 62 | 61 | 68 | 65 | 65 |
| Élément 3 | 65 | 69 | 66 | 64 | 64 | 66 | 66 | 65 | 66 | 61 | 64 |
| Élément 4 | 66 | 65 | 64 | 64 | 66 | 67 | 63 | 61 | 68 | 69 | 67 |
Etape 1: Pour chaque échantillon on calcule sa valeur moyenne et son étendue (rappel : l’étendue est la différence entre la plus grande et la plus petite des valeurs)
| Échantillons | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Élément 1 : X1 | 64 | 62 | 64 | 64 | 67 | 67 | 62 | 62 | 65 | 69 | 64 |
| Élément 2 : X2 | 65 | 63 | 64 | 65 | 63 | 70 | 62 | 61 | 68 | 65 | 65 |
| Élément 3 : X3 | 65 | 69 | 66 | 64 | 64 | 66 | 66 | 65 | 66 | 61 | 64 |
| Élément 4 : X4 | 66 | 65 | 64 | 64 | 66 | 67 | 63 | 61 | 68 | 69 | 67 |
| X=(X1+X2+X3+X4)/4 | 65 | 64,75 | 64,5 | 64,25 | 65 | 67,5 | 63,25 | 62,25 | 66,75 | 66 | 65 |
| Étendu R= Xmax-Xmin | 2 | 7 | 2 | 1 | 4 | 4 | 4 | 4 | 3 | 8 | 3 |
Etape 2 : Calculer la moyenne des moyennes et des étendues
On calcule également la moyenne des moyennes : X=(65+64.75+64.5+...+66+65)/11 =64.93
On calcule également la moyenne des étendues : R=(2+7+2+..+8+3)/11 = 3.82
Etape 3 : Calculer les limites de contrôle
A2 , D3 et D4 sont des constantes (dites constantes de Burr 1969 ) qui dépendent de la taille des échantillons (voir tableau ci-dessous)
Dans notre cas : la taille de l'échantillon égale n=4
en utilisant la table de Burr : A2=0.729 ; D3 =0 ; D4 = 2.282
Limites de contrôles des moyennes
Limite inférieure de contrôles des moyennes x : LICx = 64,93 – 0,729*3,82 = 62,15
Limite supérieure : LSCx = 64,93 + 0,729*3,82 = 67,71
Limites de contrôle des étendues
Limite inférieure : LICr = 0*3,82= 0
Limite supérieure : LSCr = 2,282*3,82 = 8,72
Etape 4 : Tracer les graphiques
On trace alors 2 graphiques :
♦ Le graphique des moyennes (avec les valeurs des moyennes des échantillons, la moyenne
générale et les limites inférieure et supérieure)
♦ Le graphique des étendues (avec les valeurs des étendues, l’étendue moyenne et les limites
inférieure et supérieure)
De nouvelles cartes seront éditées pour les 11 prochaines mesures, avec de nouvelles limites
Etape 5 : Analyser la carte (il faut analyser les deux graphiques selon les règles suivantes )
Vous trouvez ci-dessous un modèle de carte de contrôle utilisée dans les métiers de la fabrication mécanique :
Etape 3 : Calculer les limites de contrôle
| Limites de contrôles | De la moyenne | de l’étendue |
| Limite inférieure | LICx = X – A 2 * R | LICr = D 3 * R |
| Limite supérieure | LSCx = X + A 2 * R | LSCr = D 4 * R |
A2 , D3 et D4 sont des constantes (dites constantes de Burr 1969 ) qui dépendent de la taille des échantillons (voir tableau ci-dessous)
Dans notre cas : la taille de l'échantillon égale n=4
en utilisant la table de Burr : A2=0.729 ; D3 =0 ; D4 = 2.282
Limites de contrôles des moyennes
Limite inférieure de contrôles des moyennes x : LICx = 64,93 – 0,729*3,82 = 62,15
Limite supérieure : LSCx = 64,93 + 0,729*3,82 = 67,71
Limites de contrôle des étendues
Limite inférieure : LICr = 0*3,82= 0
Limite supérieure : LSCr = 2,282*3,82 = 8,72
 |
| Table de Burr 1969 |
On trace alors 2 graphiques :
♦ Le graphique des moyennes (avec les valeurs des moyennes des échantillons, la moyenne
générale et les limites inférieure et supérieure)
♦ Le graphique des étendues (avec les valeurs des étendues, l’étendue moyenne et les limites
inférieure et supérieure)
De nouvelles cartes seront éditées pour les 11 prochaines mesures, avec de nouvelles limites
Dans la feuille de calcul ci-jointe, On vous suggère une template pour construire aisément et rapidement les cartes de contrôle les plus utilisées dans le domaine à savoir : la carte nP , la carte C et la carte X-R ; et un dernier onglet pour le calcul de Capabilité Cp et Cpk. (voir l'onglet consignes dans le feuille de calcul pour plus d'informations)
Minitab est un logiciel payant de statistiques. Il est développé par Minitab Inc. pour le système d'exploitation Windows (xp,seven,8,10) uniquement. Il est largement utilisé par les universités pour enseigner les statistiques, la version commerciale du logiciel est surtout destinée aux entreprises souhaitant améliorer leur performance selon la méthode « Six Sigma ».
Pour obtenir Minitab17 (complet et gratuitement) : Laisser un commentaire
Exemple :
Nous reprenons l'exemple de carte X-R traité précédemment où on a pris 11 prélèvements (nombre d'échantillon m=11 échantillons) , chaque prélèvement comporte 4 individus (taille d'échantillon n=4)
Saisi de données sous Minitab17
Dans l'onglet "worksheet1" nous saisissons les données dans un le tableau de 11 lignes et 4 colonnes comme suit :
Choix du type de carte et des données:
Ensuite, on choisit le type de la carte qu'on veut construire dans l'onglet "STAT" dans le menu principal :
Dans l'onglet qui s'ouvrira, on choisit la plage de données, à représenter dans notre carte, qui figurent entre la colonne 'individu 1' jusqu'à la colonne 'individu 4' (en écrivant: 'individu 1'-'individu 4' ).
On peut personnaliser les règles de contrôle par cliquer sur "Xbar-R Options" ou (Alt + p) puis cliquer sur "Tests"
En cliquant sur le bouton "OK" la carte X-R s'affiche comme suit :
Pour obtenir Minitab17 (complet et gratuitement) : Laisser un commentaire
Minitab propose de nombreuses cartes de contrôle pour répondre à vos besoins en matière de contrôle de procédé; l'article suivant vous présente les cartes de contrôle supportées et comment les construire par Minitab17 :
Article Externe : Quelles sont les cartes de contrôle incluses dans Minitab ?
Exemple :
Nous reprenons l'exemple de carte X-R traité précédemment où on a pris 11 prélèvements (nombre d'échantillon m=11 échantillons) , chaque prélèvement comporte 4 individus (taille d'échantillon n=4)
Saisi de données sous Minitab17
Dans l'onglet "worksheet1" nous saisissons les données dans un le tableau de 11 lignes et 4 colonnes comme suit :
Ensuite, on choisit le type de la carte qu'on veut construire dans l'onglet "STAT" dans le menu principal :
On peut personnaliser les règles de contrôle par cliquer sur "Xbar-R Options" ou (Alt + p) puis cliquer sur "Tests"
En cliquant sur le bouton "OK" la carte X-R s'affiche comme suit :
La carte I-mR
Utilisé le plus souvent lors de production en petite série ou à très forte valeur ajoutée, elle s’applique uniquement pour des données mesurables sur des échantillons unitaires.
Utilisé le plus souvent lors de production en petite série ou à très forte valeur ajoutée, elle s’applique uniquement pour des données mesurables sur des échantillons unitaires.
La carte C
La carte C va permettre de compter le nombre de défaut pour des échantillons constants.
La carte C va permettre de compter le nombre de défaut pour des échantillons constants.
La carte NP
La carte np est la même que la carte p mais dans les cas où nous avons des échantillons constants (de taille constante N).
La carte U
Cette carte va comptabiliser le même paramètre que la C, mais le transforme en proportion.
La carte P
La carte P va nous permettre de suivre la proportion de rebuts dans des échantillons de tailles variables.
La carte Xbar-S
La carte Xbarre-S représente la moyenne des données avec l’écart-type de ces mêmes données. On l’utilise pour des données mesurables, dans le cadre de production moyenne et grande série.
La carte Xbar-R
La carte Xbarre-R est le pendant de la carte I-mR lorsque nous avons des sous-groupes.
La carte EWMA
Peu connue, cette carte présente pour autant de très nombreux avantages par rapports aux cartes traditionnelles de Shewhart.
La carte CUSUM
La carte Cusum est encore plus performante que la carte EWMA mais sa mise en œuvre et son interprétation sont plus complexes. Son utilisation est donc à réserver à des cas bien particuliers où la précision est essentielle.
La carte np est la même que la carte p mais dans les cas où nous avons des échantillons constants (de taille constante N).
La carte U
Cette carte va comptabiliser le même paramètre que la C, mais le transforme en proportion.
La carte P
La carte P va nous permettre de suivre la proportion de rebuts dans des échantillons de tailles variables.
La carte Xbar-S
La carte Xbarre-S représente la moyenne des données avec l’écart-type de ces mêmes données. On l’utilise pour des données mesurables, dans le cadre de production moyenne et grande série.
La carte Xbar-R
La carte Xbarre-R est le pendant de la carte I-mR lorsque nous avons des sous-groupes.
La carte EWMA
Peu connue, cette carte présente pour autant de très nombreux avantages par rapports aux cartes traditionnelles de Shewhart.
La carte CUSUM
La carte Cusum est encore plus performante que la carte EWMA mais sa mise en œuvre et son interprétation sont plus complexes. Son utilisation est donc à réserver à des cas bien particuliers où la précision est essentielle.
0 Commentaires